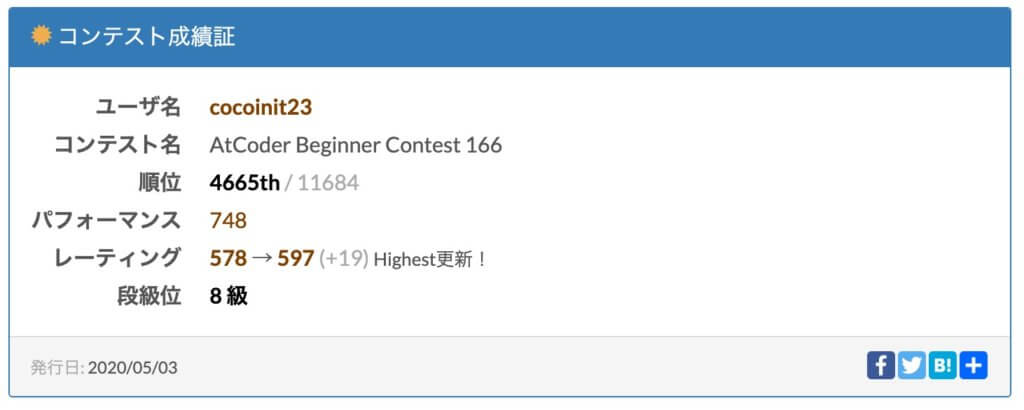
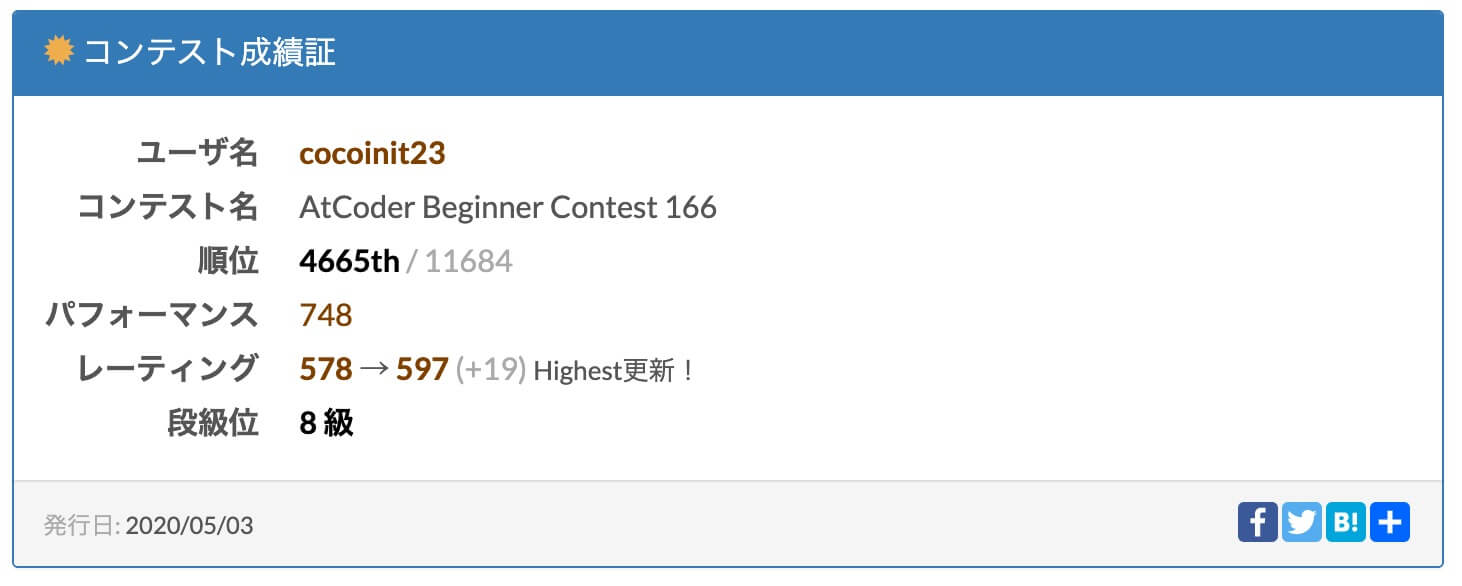
ABC166に参加した。

AtCoder Beginner Contest 166 - AtCoder
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
A – A?C
文字列の比較。
s = input()
if s == 'ABC':
print('ARC')
else:
print('ABC')
B – Trick or Treat
お菓子を持っているかどうかのフラグを格納する配列を更新しながら総当り。
n, k = map(int, input().split())
d = []
a = []
for i in range(k):
d.append(int(input()))
a.append(list(map(int, input().split())))
ans = [1] * n
for x in a:
for i in x:
ans[i - 1] = 0
print(sum(ans))
C – Peaks
どの展望台同士が繋がっているのかグラフにし、良い展望台かどうかのフラグを格納した配列を更新していく。
リストの添字を1つずらして計算するのが面倒だったので、あえて配列を1つ増やし、入力した値がそのまま添字に使えるように工夫。
Pythonで学ぶアルゴリズムの本を読んどいて良かった。
n, m = map(int, input().split())
h = [-1] + list(map(int, input().split()))
ab = [list(map(int, input().split())) for _ in range(m)]
link = [[] for _ in range(n + 1)]
for x in ab:
a, b = x[0], x[1]
link[a].append(b)
link[b].append(a)
ans = [0] + [1] * n
for i in range(len(link)):
for j in link[i]:
if h[i] <= h[j]:
ans[i] = 0
print(sum(ans))
D – I hate Factorization
A^5 – B^5 = X, 1≤X≤10^9 の制約。
10^9 をざっくり5乗根取ると 10^2 より小さいぐらいになる。
多めに 10^4で余裕を持って正負の値を全探索。
A^5 も B^5 も奇関数なので、実際には正の値だけの探索でOK。
x = int(input())
for a in range(-1000, 1000):
for b in range(-1000, 1000):
if a ** 5 - b ** 5 == x:
print(a, b)
exit()
E – This Message Will Self-Destruct in 5s
本番中に解けなかったのでコンテスト後AC。
条件を満たすペアを i, j ( i<=j ) とるすと、条件式は j – i = A[ i ] + A[ j ] となる。
移項して i + A[ i ] = j – A[ j ] を満たす i, j の数を求めれば良い。
i + A[ i ] と i – A[ i ] の配列をそれぞれx, y として事前に計算しておき、同じ値を持つ組み合わせを計算する。
from collections import Counter
n = int(input())
a = list(map(int, input().split()))
x = [0] * n
y = [0] * n
for i in range(n):
x[i] = i + a[i]
y[i] = i - a[i]
cx = Counter(x)
cy = Counter(y)
ans = 0
for i in cx.keys():
ans += cx[i] * cy[i]
print(ans)
入力例1の場合、
cx : Counter({4: 2, 2: 1, 5: 1, 7: 1, 6: 1})
cy : Counter({-2: 2, -1: 1, 2: 1, 1: 1, 4: 1})
となる。
共通する値である2と4を、x, y のそれぞれから選ぶ組み合わせ数を求めるので、
2 を選ぶ組み合わせ : 1 x 1
2 を選ぶ組み合わせ : 2 x 1
となり、答えは3となる。
次でレート600になれるかな?

コメント