リアルタイムで参加しました。

A – Edge Checker
線で結ばれていれば隣り合っているはずなので、差が1になる組み合わせが答え。
そのまま差を取ると両端の場合がコーナーケースになるので、場合分けを追加。
a, b = map(int, input().split())
if b - a == 1:
print('Yes')
elif a == 1 and b == 10:
print('Yes')
else:
print('No')B – Count Distinct Integers
重複しない要素はsetで扱える。
n = int(input())
a = list(map(int, input().split()))
ans = len(set(a))
print(ans)C – Jumping Takahashi
最初はDPかと思ったが、C問題でDPが出るわけ無いと思いこんでしまい全探索した。
O(2^N)なのでTLEするはずなのだが、何故か通ってしまった。恐らく嘘解法。
N回目のジャンプで位置Xにいないとだめなので、Xを超えたら終了する。
2進む→1進む、1進む→2進む、のように、同じ位置に来るケースが考えられるので、setで重複を省いておく。
n, x = map(int, input().split())
pos = [0]
for _ in range(n):
a, b = map(int, input().split())
temp = []
for i in pos:
if i + a <= x:
temp.append(i + a)
if i + b <= x:
temp.append(i + b)
pos = list(set(temp))
if not pos:
break
print('Yes' if x in pos else 'No')想定解であろうDPで解いてみる。
i回目のジャンプで位置jにいる場合、i+1回目はj+aまたはj+bに移動できる。
dp[i][j]として、ジャンプした回数と位置を更新していく。
スタート地点は0回目のジャンプで位置0にいるので、dp[0][0]=Trueが初期値。
配列外参照に注意しつつDPを行う。
ジャンプ毎に位置jにいるかどうか判定していくので、計算量はO(NX)
n, x = map(int, input().split())
dp = [[False] * (x + 1) for _ in range(n + 1)]
dp[0][0] = True
for i in range(n):
a, b = map(int, input().split())
for j in range(x + 1):
if dp[i][j]:
if j + a <= x:
dp[i + 1][j + a] = True
if j + b <= x:
dp[i + 1][j + b] = True
ans = dp[n][x]
print('Yes' if ans else 'No')位置xにいるかどうかは0か1で判定出来るので、ビット演算を使っても解くことが出来る。
位置iにいる時、a移動するという処理を、1になっているビットをa個シフトさせると考える。
スタート地点を 0001 とすると、1移動すると 0010 になり、2移動すると 0100 になる。
これのORを取ると 0110 となり、スタート地点から1または2移動したケースと等しくなる。
これを繰り返していき、xビット目が1になったら移動可能であると判定できる。
移動する際は左シフトさせていくので、xにいるかどうかは右シフトで戻せばOK。
n, x = map(int, input().split())
dp = 1
for i in range(n):
a, b = map(int, input().split())
a = dp << a
b = dp << b
dp = a | b
ans = (dp >> x) & 1
print('Yes' if ans else 'No')C問題にしては難しい?
D – Strange Balls
スタックを使って問題文通りに実装する。
最初のボールをスタックの初期値とする。
このボールが消えることはないので、答えの1をまずは出力する。
n = int(input())
a = list(map(int, input().split()))
stack = [[a[0]]]
print(1)次にスタックのループを考える。
同じボールが連続すれば消え、違うボールだったら消えないので、ifで分岐させる必要がある。
同じボールが連続するという部分は、1つ前のボールと同じかどうかの判定を繰り返すと考える。
ボールが消える処理があるため、スタックが空になる場合も考える。
以上よりメインルーチンの大枠は以下の通り。
prev = None
ans = 1
for i in a[1:]:
if stack:
prev = ...
if i == prev:
...
else:
...
else:
...
print(ans)整数kが書かれたボールがk個連続すると消えてしまうため、(値、個数)というタプルをスタックに積み込みたくなる。
しかし、タプルになると実装が少し面倒なのと、リストの長さlenはO(1)で求まるため、同じ値のボールは同じ配列にまとめてしまうこととする。
例えば、[2], [3,3],[4,4],[3],… という感じ。
prev = None
ans = 1
for i in a[1:]:
if stack:
prev = stack[-1][0]
if i == prev:
...
else:
stack.append([i])
prev = i
ans += 1
else:
stack.append([i])
prev = i
ans += 1
print(ans)配列を積み込んでいくので、最新のボールの値はstack[-1][0]、個数はlen(stack(-1))で求まり、いずれもO(1)で得られる。
あとは、整数kが書かれたボールがk個連続しているかどうか判定し、スタックから除去するかどうか処理していく。
n = int(input())
a = list(map(int, input().split()))
stack = [[a[0]]]
print(1)
prev = None
ans = 1
for i in a[1:]:
if stack:
prev = stack[-1][0]
if i == prev:
stack[-1].append(i)
ans += 1
if len(stack[-1]) == i:
stack.pop()
ans -= i
else:
stack.append([i])
prev = i
ans += 1
else:
stack.append([i])
prev = i
ans += 1
print(ans)E – Ranges on Tree
グラフを区間に置き換える問題。
オイラーツアーやセグメントツリーに少し似ている。
ある頂点からなる部分木を考えた時、子の区間を全て含むように親の区間を更新していく。
最大値が最小のものを求められているので、出来るだけ小さい区間を与えていくことを考え、葉の部分はL=Rとする所から考える。
葉の個数が区間の幅となる。葉が5つあればL=1、R=5になる。
親の区間は、部分木の左端から右端になるようにすればいいので、子の最小のLと、最大のRを持てばいい。
公式解説の図がわかりやすいので引用。
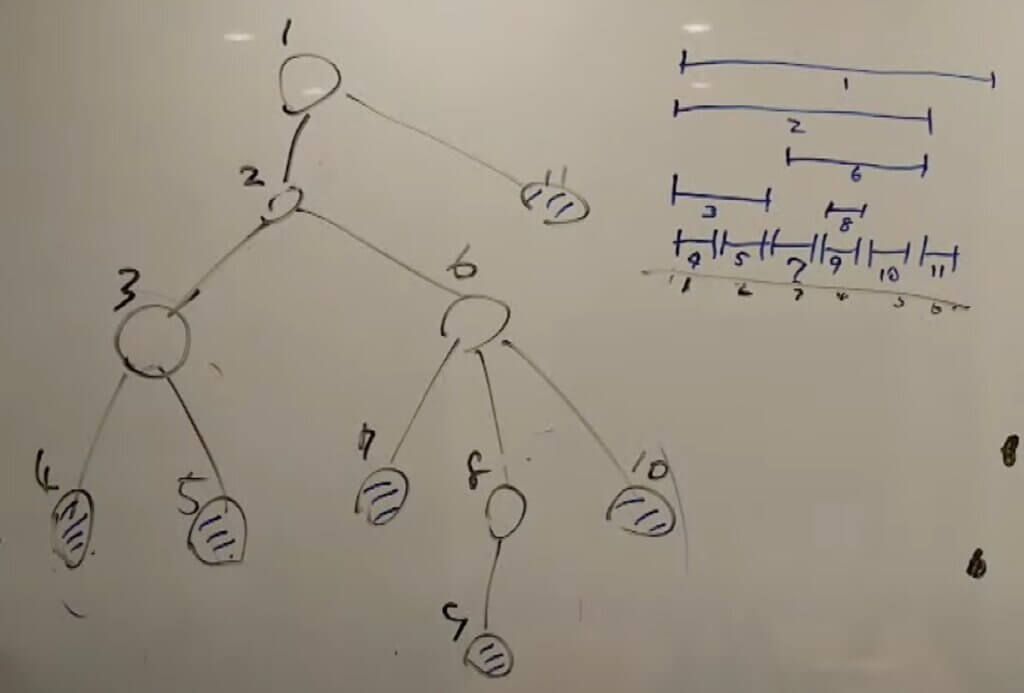
子から親に戻っていくため、深さ優先探索(DFS)を考える。
葉の数を数える変数を用意し、葉にたどり着いたら加算していく。
答えのL、Rを保存する配列を用意し、再起の上限数を伸ばすおまじないを書く。
import sys
sys.setrecursionlimit(10 ** 6)
n = int(input())
graph = [[] for _ in range(n + 1)]
for _ in range(n - 1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
num_leaf = 0
l = [1e9] * (n + 1)
r = [0] * (n + 1)まず、子のことを考えなくてもいい葉にたどり着いた所の簡単な処理から考える。
DFSの引数に親の情報を持たせることで、葉かどうかの判定がやりやすくなる。
def dfs(vertex, parent):
if graph[vertex] == [parent]:
num_leaf += 1
l[vertex] = num_leaf
r[vertex] = num_leaf次に、子がある場合を考える。
子の情報を更新してから親の情報を更新したいので、先にDFSで潜ってから情報を更新していく。
else:
min_l = num_leaf + 1
max_r = num_leaf + 1
for next_v in graph[vertex]:
if next_v == parent:
continue
dfs(next_v, vertex)
min_l = min(min_l, l[next_v])
max_r = max(max_r, r[next_v])全ての子のDFSが終わった後で、親の答えを更新する。
l[vertex] = min_l
r[vertex] = max_rpypyの再起は遅いので、pythonで提出するように注意する。
import sys
sys.setrecursionlimit(10 ** 6)
n = int(input())
graph = [[] for _ in range(n + 1)]
for _ in range(n - 1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
num_leaf = 0
l = [1e9] * (n + 1)
r = [0] * (n + 1)
def dfs(vertex, parent):
global num_leaf, l, r
if graph[vertex] == [parent]:
num_leaf += 1
l[vertex] = num_leaf
r[vertex] = num_leaf
else:
min_l = num_leaf + 1
max_r = num_leaf + 1
for next_v in graph[vertex]:
if next_v == parent:
continue
dfs(next_v, vertex)
min_l = min(min_l, l[next_v])
max_r = max(max_r, r[next_v])
l[vertex] = min_l
r[vertex] = max_r
dfs(1, 0)
for i in range(1, n + 1):
print(l[i], r[i])これを提出すると1167msだった。

再起にするから遅いのであって、スタックでwhileに書き換えればpypyで高速化できるはず。
葉にたどり着いた時の行きがけに葉のLとRの配列を更新し、親の帰りがけに親のLRを更新すればOK。
便宜的に、行きがけの判定は頂点が正の値の時、帰りがけの判定は頂点が負の値とする。
こうすると行きがけ帰りがけのフラグを持ったタプルにする必要がなくなって実装が簡単になる。
スタックは先入れ後出しなので、帰りがけ→行きがけの順でスタックに積みこんでいくことに注意する。
n = int(input())
graph = [[] for _ in range(n + 1)]
for _ in range(n - 1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
num_leaf = 0
l = [1e9] * (n + 1)
r = [0] * (n + 1)
stack = [(~1, 0), (1, 0)] # 帰りがけを先に積む
while stack:
curr, prev = stack.pop()
if curr > 0: # 行きがけ
if graph[curr] == [prev]:
num_leaf += 1
l[curr] = num_leaf
r[curr] = num_leaf
else:
stack.append([~curr, None]) # 帰りがけを先に積む
for next_v in graph[curr]:
if next_v == prev:
continue
stack.append([next_v, curr])
else: # 帰りがけ
curr = ~curr # 符号を戻す
for child_v in graph[curr]:
l[curr] = min(l[curr], l[child_v])
r[curr] = max(r[curr], r[child_v])
for i in range(1, n + 1):
print(l[i], r[i])671msとなり、pythonの再起よりも2倍早くなった。





コメント