AtCoder Beginner Contest 179の感想

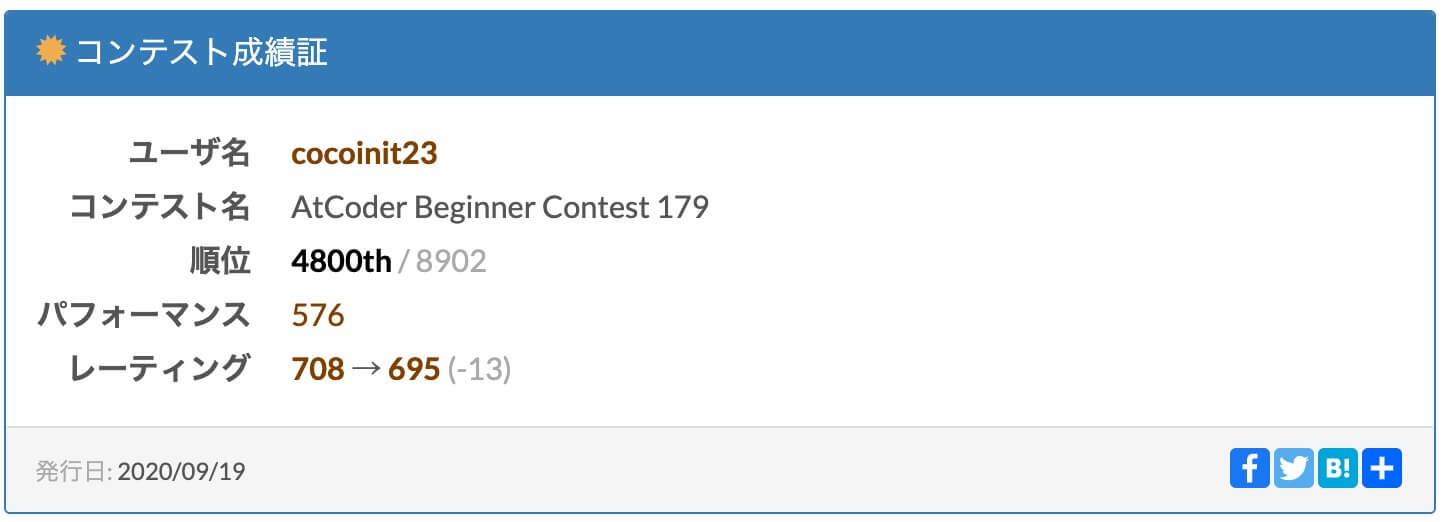
ABC179に参加した。

A – Plural Form

やるだけ。

Pythonは足し算みたいに文字列を扱えるので楽ちん。

s = input()

print(s + 's') if s[-1] != 's' else print(s + 'es')

B – Go to Jail

d1=d2の個数を数えていき、d1≠d2になったらカウントをリセットする。

n = int(input())

count = 0
ans = False
for i in range(n):
    d1, d2 = map(int, input().split())
    if d1 == d2:
        count += 1
    else:
        count = 0

    if count == 3:
        ans = True
        break

print('Yes') if ans else print('No')

C – A x B + C

A x B = N – C と変形した場合、A x B が決まれば C も自動的に決まる。

A を固定した時に B が何個あるのかを高速で求めたい問題に変わる。

A x B = N – C <= N – 1 なので、B は最大でも ( N – 1 ) / A となることを利用すると、O(N)で計算できる。

n = int(input())

ans = 0
for a in range(1, n):
    ans += (n - 1) // a

print(ans)

D – Leaping Tak

本番中は愚直なDPしか実装できずTLEでWA。

愚直なDPだとO(N^2)となり間に合わないが、区間の和という単語に注目すると累積和が適応できそうだと分かる。

区間ごとにDPを更新していき、最後に累積和の配列を更新するとO(NK)で答えを出すことができた。

n, k = map(int, input().split())
mod = 998244353
lr = [list(map(int, input().split())) for _ in range(k)]

dp = [0] * (n + 10)
dp[1] = 1
cumsum = [0] * (n + 10)
cumsum[1] = 1

for i in range(2, n + 1):
    for l, r in lr:
        if l >= i:
            continue

        ll = max(1, i - r)
        rr = i - l
        dp[i] += cumsum[rr] - cumsum[ll - 1]
        dp[i] %= mod
    cumsum[i] = cumsum[i - 1] + dp[i]
    cumsum[i] %= mod

print(dp[n] % mod)

C問題に時間がかかり、D問題を解けかなったのでパフォーマンスは振るわなかった。