1155. Number of Dice Rolls With Target Sum

Just a moment...

k面のサイコロをn個振った時、合計値がtargetになる組み合わせの数を求める問題。

全探索する場合、1~kのどれが出るかという試行がn回繰り返され、O(K^N)となり間に合わない。

ここで、サイコロの出目を1つずつ足していくことを考える。

サイコロn個振った時の出目は、n-1個の出目が出た状態でもう1個サイコロを振ると考えられる。

以下同様に、1個前の状態に戻って行くことを考えると、DPで解けそうな気がしてくる。

必要な情報は、何個目のサイコロを振ったか、合計値はいくつか、何通りの組み合わせがあるのか、の3つである。

そのため、DPを以下のように設定する。

DP[dice][val] = ways

dice : サイコロを振った回数

val : 出目の合計

ways : 組み合わせの合計数

このDPテーブルを更新していくことを考える。

まずはDPの初期化。今回の問題は余りを求めるため、modも用意。

1-indexで考えるほうが直感的なので、配列数は+1している。

class Solution:
    def numRollsToTarget(self, n: int, k: int, target: int) -> int:
        dp = [[0] * (target + 1) for _ in range(n + 1)]
        mod = 10 ** 9 + 7

次に遷移を考える。

脳内ではイメージしにくいため、手書きして実験してみる。

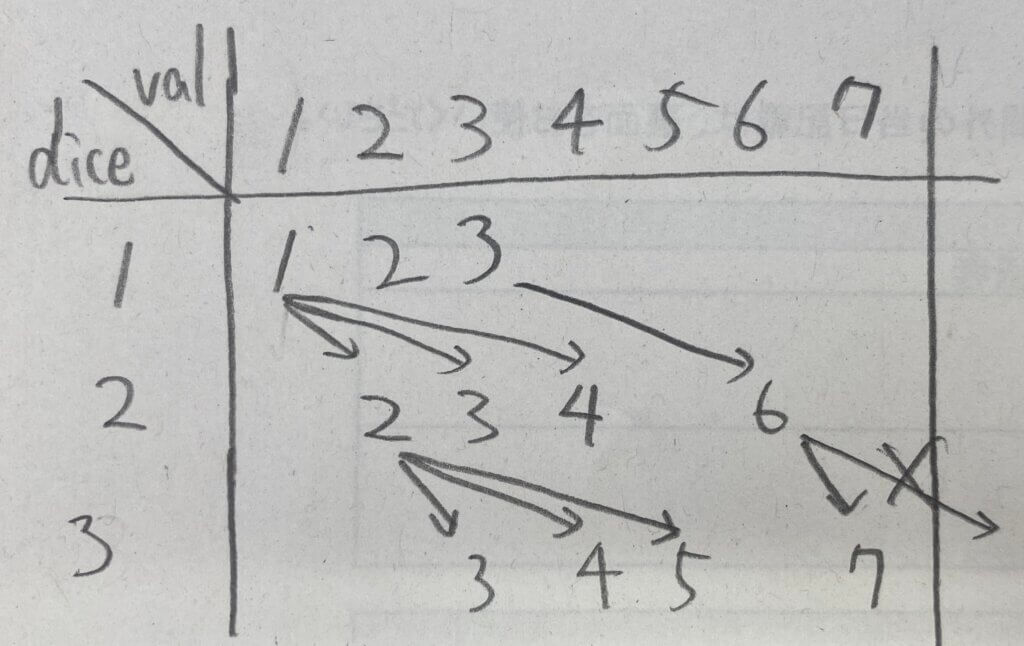
合計n個のサイコロを振った時、起こりうる出目の合計値は・・・

最小値は全部1が出た場合、1 * n

最大値は全部kが出た場合、k * n

ただし、求めたい値は合計値がtargetになるケースなので、最大値がtargetを超えた場合は min(k * n, target) としてクリップする必要がある。

以上からDPを更新するループは以下のようになる。

        for dice in range(1, n + 1):
            for val in range(dice, min(k * dice, target) + 1):

サイコロが1個の時は1通りしかない。

                if dice == 1:
                    dp[dice][val] = 1

サイコロが2個以上の時、前回までの合計値から遷移してくる。

出目の値は1〜kなので、val-1 〜 val-k から遷移してくる。

ただし、val-kは配列外参照になる可能性があるため、max(1, val-k)とする。

                else:
                    end = val - 1
                    start = max(1, val - k)
                    dp[dice][val] = sum(dp[dice - 1][start:end + 1]) % mod

n回目にtargetになる組み合わせの数を返して終わり。

全部のコードを繋げると以下の通り。

class Solution:
    def numRollsToTarget(self, n: int, k: int, target: int) -> int:
        dp = [[0] * (target + 1) for _ in range(n + 1)]
        mod = 10 ** 9 + 7

        for dice in range(1, n + 1):
            for val in range(dice, min(k * dice, target) + 1):
                if dice == 1:
                    dp[dice][val] = 1
                else:
                    end = val - 1
                    start = max(1, val - k)
                    dp[dice][val] = sum(dp[dice - 1][start:end + 1]) % mod

        ans = dp[n][target] % mod

        return ans

時間計算量は2重ループの部分でO(NK)、空間計算量はDPテーブルの部分でO(NK)となる。